LES Methods & Applications
Large Eddy Simulation
Currently, most computations used for the prediction of turbulent flows are based on the Reynolds-Averaged Navier-Stokes (RANS) equations. However, RANS computations predict only flow averages, and require additional models to account for the effects of turbulence. As the latter tend to be calibrated for specific areas of application, the predictive ability of RANS is often limited,particularly when considering unusual or complex flows. Large-eddy simulation (LES), in which the largest of the unsteady turbulent flow features are resolved, is a more expensive but effective alternative for flow-physics research and predictive engineering design. Successful LES requires the simultaneous computation of a significant range of turbulent length and time scales, and thus requires both efficient numerical methods and high-performance computing technology. As a reward, one may examine a much wider range of flow conditions, including those featuring separation, chemical reactions, or novel flow control devices. The dynamic information provided by LES is also valuable for applications in transition, combustion, and sound prediction.
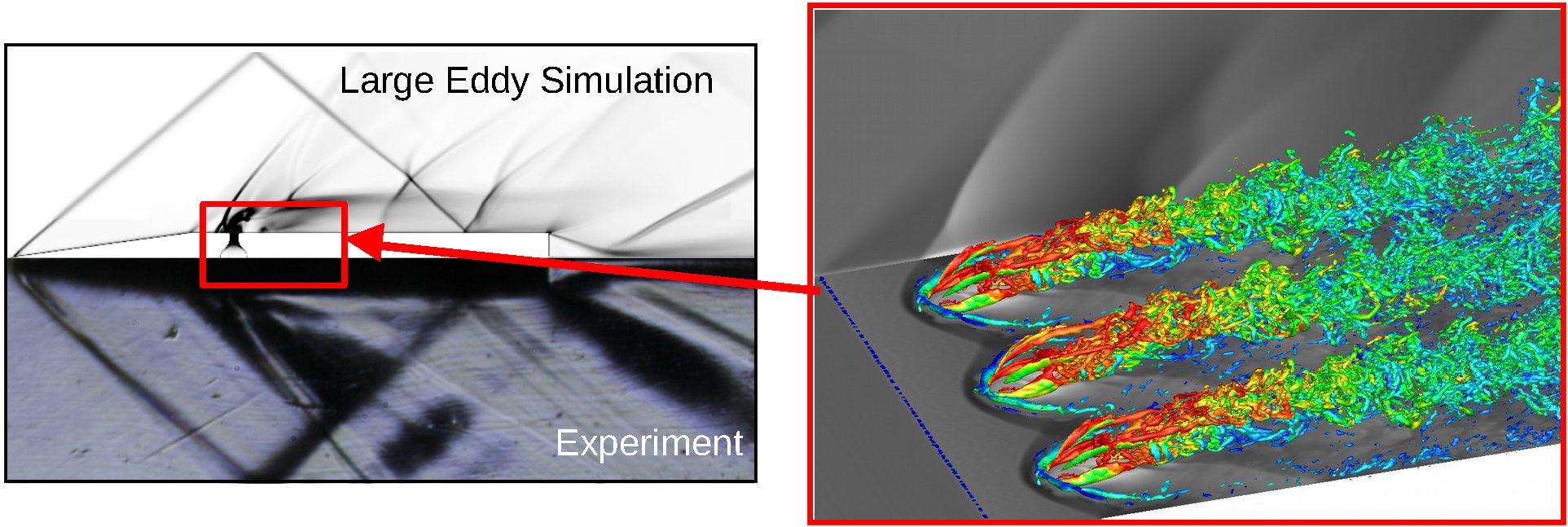
The Aerodynamics group is actively involved in both fundamental and applied research related to the large-eddy simulation (LES) of turbulent flows. Our focus is on designing and developing new numerical techniques in the context of challenging engineering problems, including those involving multiphase, compressible, and reacting turbulent flows. An overview of some of our our current research topics is given below.
Turbulent Cavitating Flows
The development of efficient combustion processes and the reduction of emissions requires a detailed understanding of the physical phenomena occurring within an engine design. For engines using injectors, this can include local evaporation (cavitation) followed by the collapse of the resulting vapour structures. When collapses occur near a solid wall, intense shock waves and liquid jets are created. These can lead to the erosion of engine components, but can also be used to clean surface deposits and promote primary jet breakup.
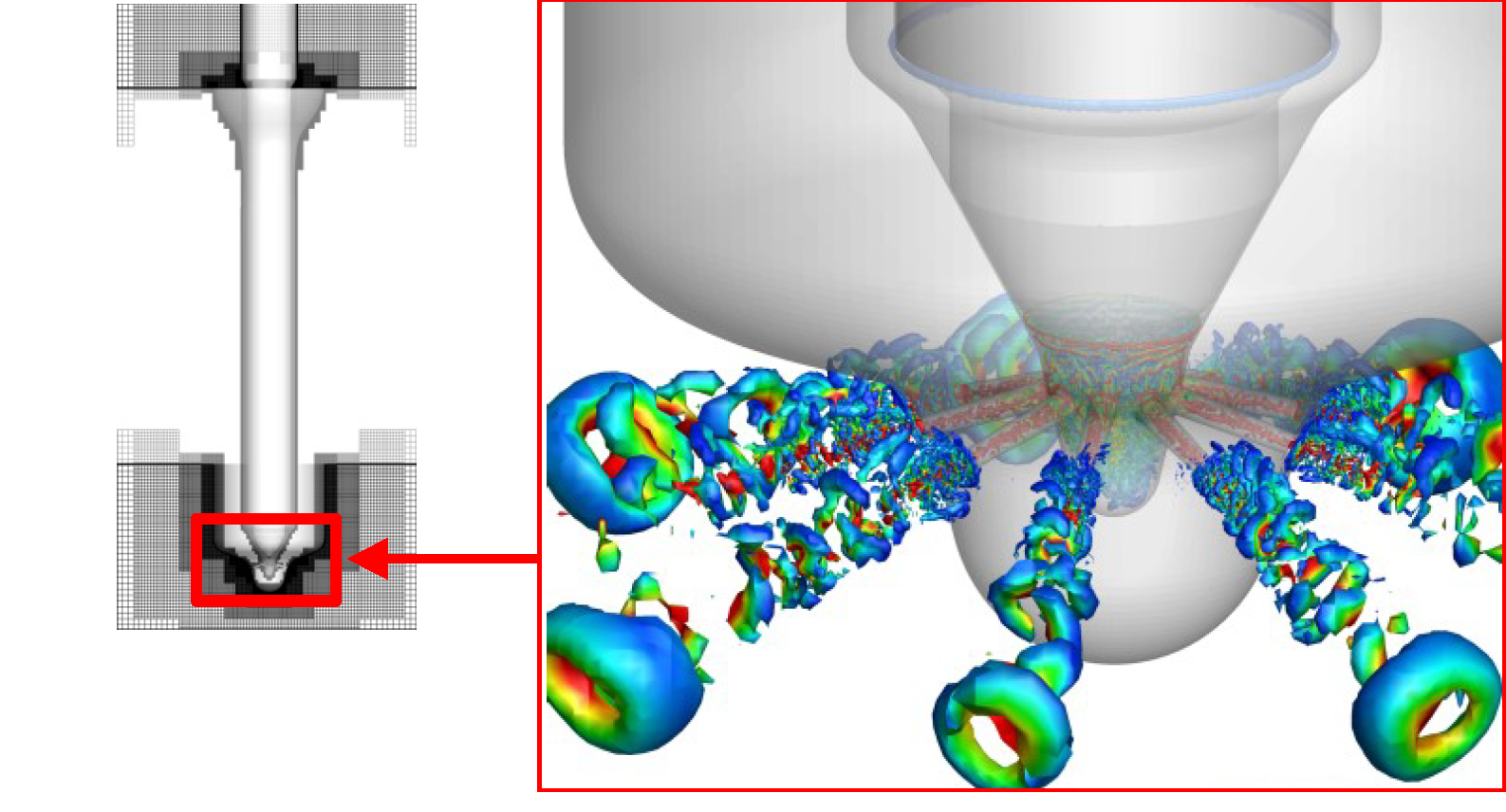
Resolving phenomena similar to those shown in figure 2 require computations on very refined meshes (in this case exceeding 100 million cells). These must be performed using time steps small enough to resolve sound waves in the liquid phase, yet for times long enough to permit the simulation of the complete injection cycle. To make such a problem tractable, highly efficient numerical methods must be used. In this case, a non-linear finite volume method was used, based on flux reconstructions which allow truncation errors to function as a physically consistent subgridscale models (Hickel, Êgerer and Larsson, Physics of Fluids, 2014). This was implemented within an immersed boundary method (Örley, Pasquariello, Hickel and Adams, Journal of Computational Physics, 2015) to facilitate the movement of system components. For more information contact S.Hickel@TUDelft.NL.
Compressible Reacting Flows
Interactions between shock waves and density gradients induce Richtmyer-Meshov instabilities (RMI), which lead to baroclinic vorticity production, followed by Kelvin Helmholtz instabilities (KMI) leading to intricate mixing processes. In presence of reactive components, ignition arising due to local regions of high pressure and temperature results in deflagration and detonation waves which can significantly influence the mixing process. Understanding the mechanisms involved requires high-resolution 3D simulations with detailed chemistry.

For problems of this type we solve the full set of compressible reacting multi-component Navier-Stokes equations, leading to results similar to those shown in figure 3. Comparison of reacting shock-bubble interactions with their inert counterparts has revealed that the supersonic detonation wave in the reacting flow suppresses the growth of secondary instabilities, and can reduce mixing by up to 40%. For more information contact S.Hickel@TUDelft.NL.
Shock Wave Boundary Layer Interactions
Shock wave boundary layer interactions (SWBLI) occur in a wide range of engineering flow devices, including supersonic air intakes, turbomachinery cascades, and over-expanded nozzles. When they induce separation, the resulting flow dynamics are relatively low frequency, potentially leading to aeroelastic coupling and structural failure. Due to the large number of dynamically relevant scales in SWBLI, however, their detailed behaviour remains difficult to predict and control.

For resolving SWBLI, we solve the 3D compressible Navier-Stokes equations using an adaptive local deconvolution method which provides a physically consistent implicit subgrid-scale model on relatively coarse meshes (Hickel, Êgerer and Larsson, Physics of Fluids, 2014. This is coupled with a shock sensor to activate the discontinuity dissipation operator. Numerical convergence has been demonstrated using meshes exceeding 700 million cells. The results have been analysed using both spectral analysis and dynamic mode decomposition techniques (Grilli, Schmidt, Hickel and Adams, Journal of Fluid Mechanics, 2012. Pasquariello, Hickel and Adams, Journal of Fluid Mechanics, 2017). The former compare well with experimental results, while the latter have been used to identify the key dynamic modes. For more information contact S.Hickel@TUDelft.NL.
Turbulence in Supercritical Fluids
Many of today's energy conversion devices operate at high pressures, in which fluid properties deviate significantly from those of an ideal gas. Examples include liquid rocket engines, highpressure Diesel engines, and stationary gas turbines operated with an organic Rankine cycle. Predicting the resulting flow fields can be particularly challenging due to the strongly non-linear changes in fluid properties close to the pseudoboiling line (Müller et al., 2016, Matheis et al., 2016).
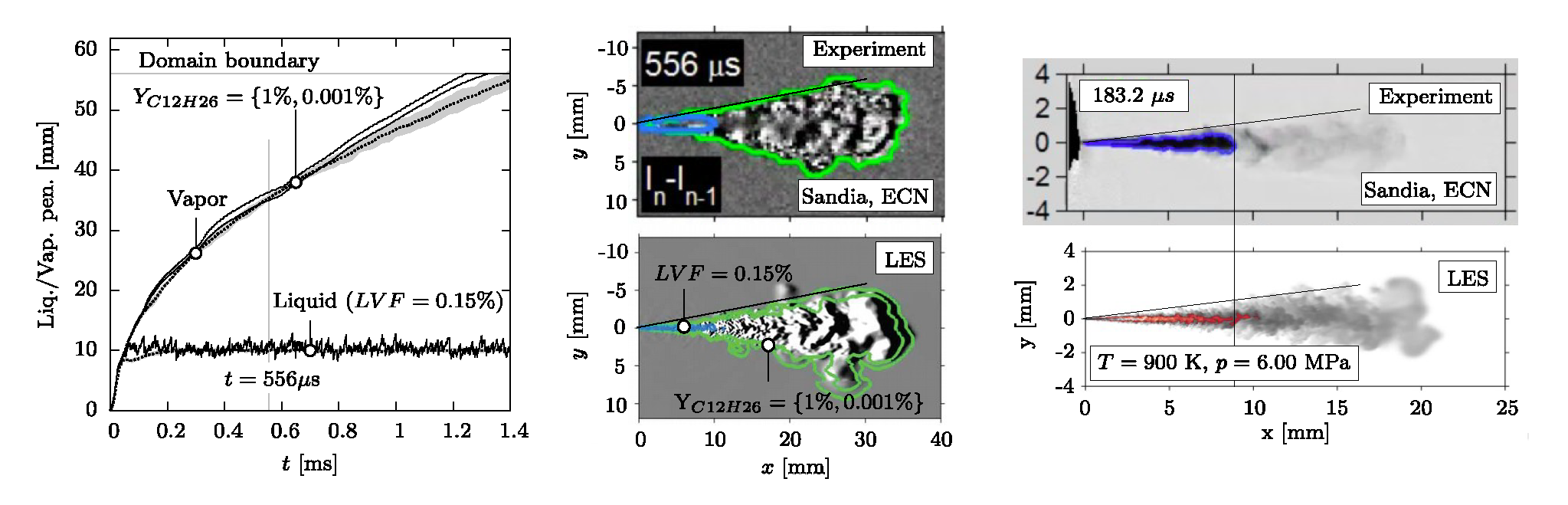
To compute such flows we have developed a detailed multi-species two-phase thermodynamic equilibrium model for liquid-fuel injection at high pressure (Matheis and Hickel, 2016, 2018). This model can represent the coexistence of supercritical states and multi-component subcritical twophase states. Comparisons with ECN Spray A experimental data have demonstrated excellent agreement, see figure 5. Both quasi- and fully conservative discretisations of the governing equations have been developed and tested. Both have been shown to converge consistently, but the conservative formulation demonstrates superior performance for the coarser meshes typical in LES. For more information contact S.Hickel@TUDelft.NL.
Adaptive Methods for High-Fidelity Simulations
Despite the increasing use of LES, it remains an expert tool. This is primarily due to the necessity of using relatively coarse grids to maintain efficiency, thereby leaving little margin for the resolution of unanticipated structure. We are addressing this issue through our work on adaptive LES, in which the flow solver dynamically adapts its local discretisation to the evolving solution without user intervention. This includes methods for the quantification and control of uncertainties that result from model approximations and numerical errors (Schranner et al., 2015, Tritschler et al. 2014) or from uncertain initial data and boundary conditions (Tritschler et al. 2014).
These methods have been implemented in our INCA reseach code, a general-purpose multi-physics solver employing hybrid MPI/OpenMP parallelisation for solving problems on thousands of processors using Cartesian grids with adaptive mesh refinement (AMR). Non conforming flow boundaries are modelled using an immersed interface method which also facilitates code coupling with structural solvers. For more information contact S.Hickel@TUDelft.NL.
Variational Multiscale Methods
Variational multiscale methods (VMM), initially developed by Hughes et al. (and pursued by several prominent groups worldwide) provide an elegant framework for developing consistent models for unresolved scales, which can be applied to arbitrary element geometries. Our work is focused on the decreasing the resolution requirements of VMM in situations where classical unresolved scale models are insufficient. In the first part of this research, we are analysing the efficacy of Variational Germano methods. These actively calibrate unresolved-scale models based on the assumption that the model should be applicable to a range of scales. The underlying assumptions of the variational Germano approach have been tested by comparing their results to optimal ones determined using goal-oriented optimisation techniques. This has allowed identification of deficiencies in the Germano approach, and provides a path to their improvement.
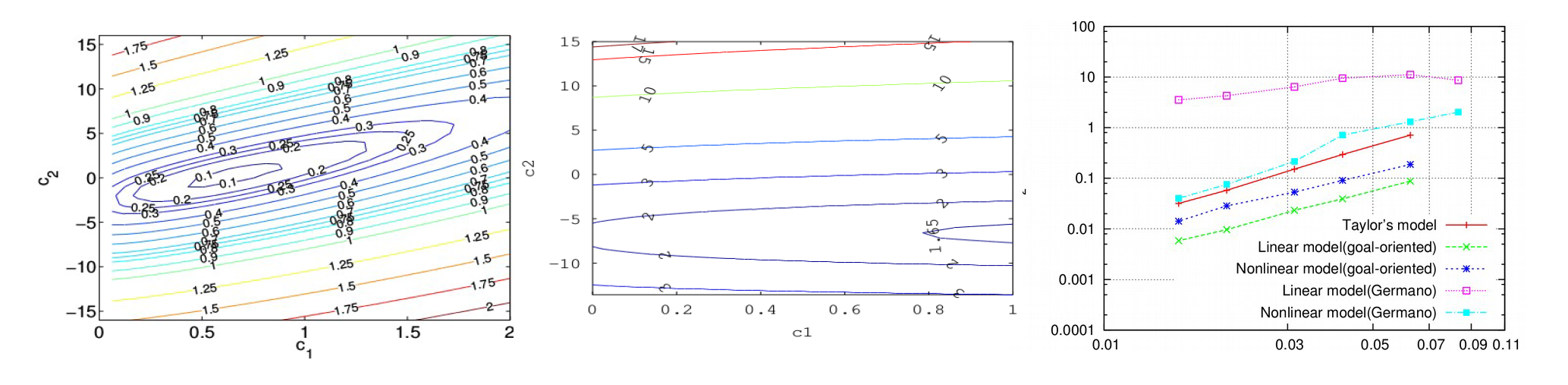
In the second part of the research, machine-learning algorithms are being exploited for model calibration. The focus of this work is on developing effective training algorithms to avoid the expensive of generating extensive reference data. For more information, contact S.J.Hulshoff@TUDelft.NL.
Optimal Reduced-Order Models
The very large number of degrees of freedom required for LES introduces difficulties aside from the basic computational cost of a simulation. The first of these is the intractable number of state variables from the perspective of control system design. The second is the difficulty of extracting causal relationships from complex high-dimensional data. To deal with these issues we have been developing goal-oriented reduced-order modelling techniques based on a continuous formulation. These allow for the definition of optimal modes corresponding to general nonlinear goal functions arising from the solution of arbitrary nonlinear PDEs.
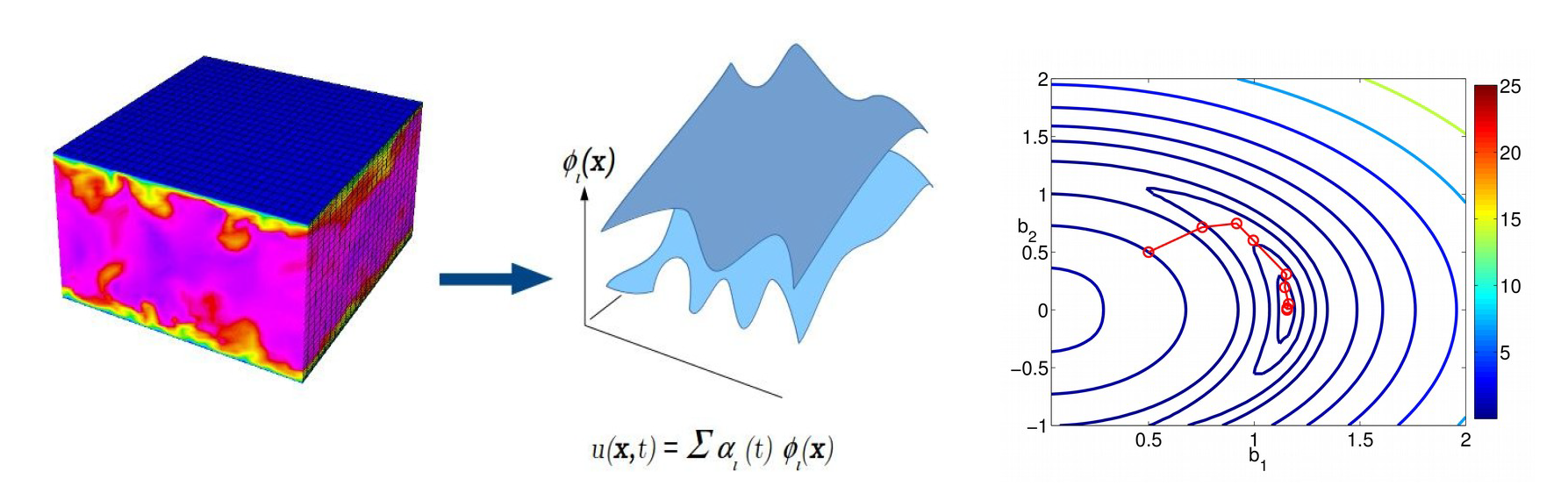
The optimal modes are found using a model-constrained optimisation process employing repeated solution of the primal and adjoint forms of the PDEs. The result is a reduced order model (ROM) which is able to predict a chosen measure of the flow with optimal accuracy for a given number of degrees of freedom. This allows for unambiguous answers to questions such as: which physical modes contribute most to a particular process under study? Significantly, this process does not have to be a function of the most energetic structures in the flow, making the technique particularly powerful for applications in transition and aeroacoustics. For more information, contact S.J.Hulshoff@TUDelft.NL.
For more information:

Dr. S.J. (Steven) Hulshoff
