Structure preserving discretization for CFD
Structure-preserving numerical methods aim to preserve physical conservation laws exactly in a discrete setting. Examples are: exact conservation of mass, conservation of kinetic energy and helicity in time. In order to establish this one needs a formulation (Lagrangians, Hamiltonians) which includes the conservation properties and appropriate finite dimensional sub-spaces in which the conserved quantities can be represented.
Spatial discretization
- Mimetic spectral element methods: Higher order methods which satisfy a discrete De Rham sequence. This allows for the conservation of many physical properties at the discrete level, see https://arxiv.org/abs/1604.00257 or https://arxiv.org/abs/1707.00346
- The use of algebraic dual polynomial spaces: In finite element methods one looks for the (optimal) solution in a linear vector space. Associated to linear vector spaces are their algebraic dual spaces. The combination of primal and dual spaces leads to:
- very sparse spectral element methods;
- parts of the system matrix which are independent of the size and shape of the mesh;
- low condition number of the resulting system
For more information see: https://arxiv.org/abs/1712.09472
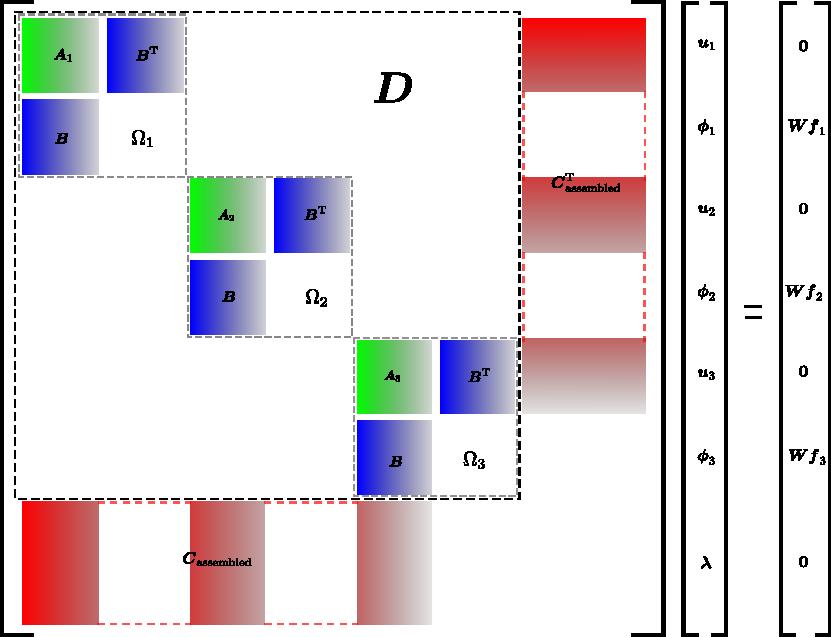
- Hybrid finite element methods: Hybrid finite element methods are based on domain decomposition techniques. These methods were proposed midway the 1960’s. By solving variables in a suitably chosen trace space, the method allows for full parallelization of the solution in the sub-domains. Furthermore, hybrid methods admit a larger class of admissible boundary conditions. In solid mechanics, for instance, both the displacements and the forces at the boundary are available. Such methods will play a role in multi-physics applications such as fluid-structure interaction or conjugate heat transfer problems.
In order to conserve certain physical quantities in time special time stepping procedures need to be developed. In the Aerodynamics group research in time-stepping techniques entails:
- Investigation of the application of Spectral Deferred Corrections (SDC), Integral Deferred Corrections (IDC) and the Picard Integral Exponential Solver (PIES) as a means to perform time integration for unsteady flow and fluid-structure interaction problems. By dividing a time interval into a number of sub-steps, an arbitrary order of accuracy can be achieved by performing a number of sweeps with a low order method over the time interval. Each sweep results in a correction to the solution. This allows the use of parallel-in-time discretization that can potentially speed up unsteady simulations on cluster computers. A second benefit is the possibility to reconstruct the solution at any point in the interval, which can be beneficial when coupling to another solver that uses a more refined time discretization, as one could encounter in fluid-structure interaction or fluid-acoustic coupling.
- Dual time integration methods to ensure conservation in time. Staggered time stepping schemes, https://arxiv.org/abs/1604.00257, energy-preserving time-stepping and symplectic time-stepping methods, https://arxiv.org/abs/1505.03422
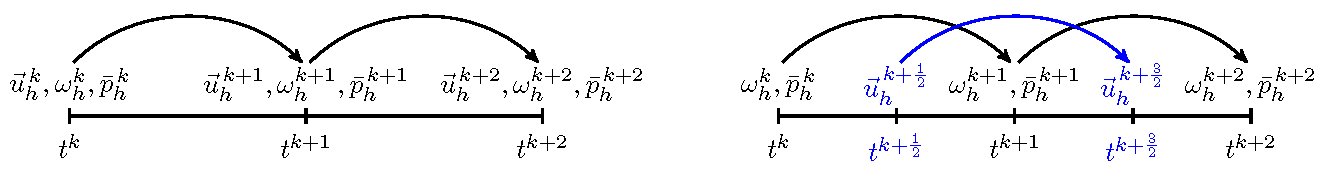
For more information:

Dr.ir. M.I. (Marc) Gerritsma
