Smooth non-parametric shape constraint estimation
Research Summary:
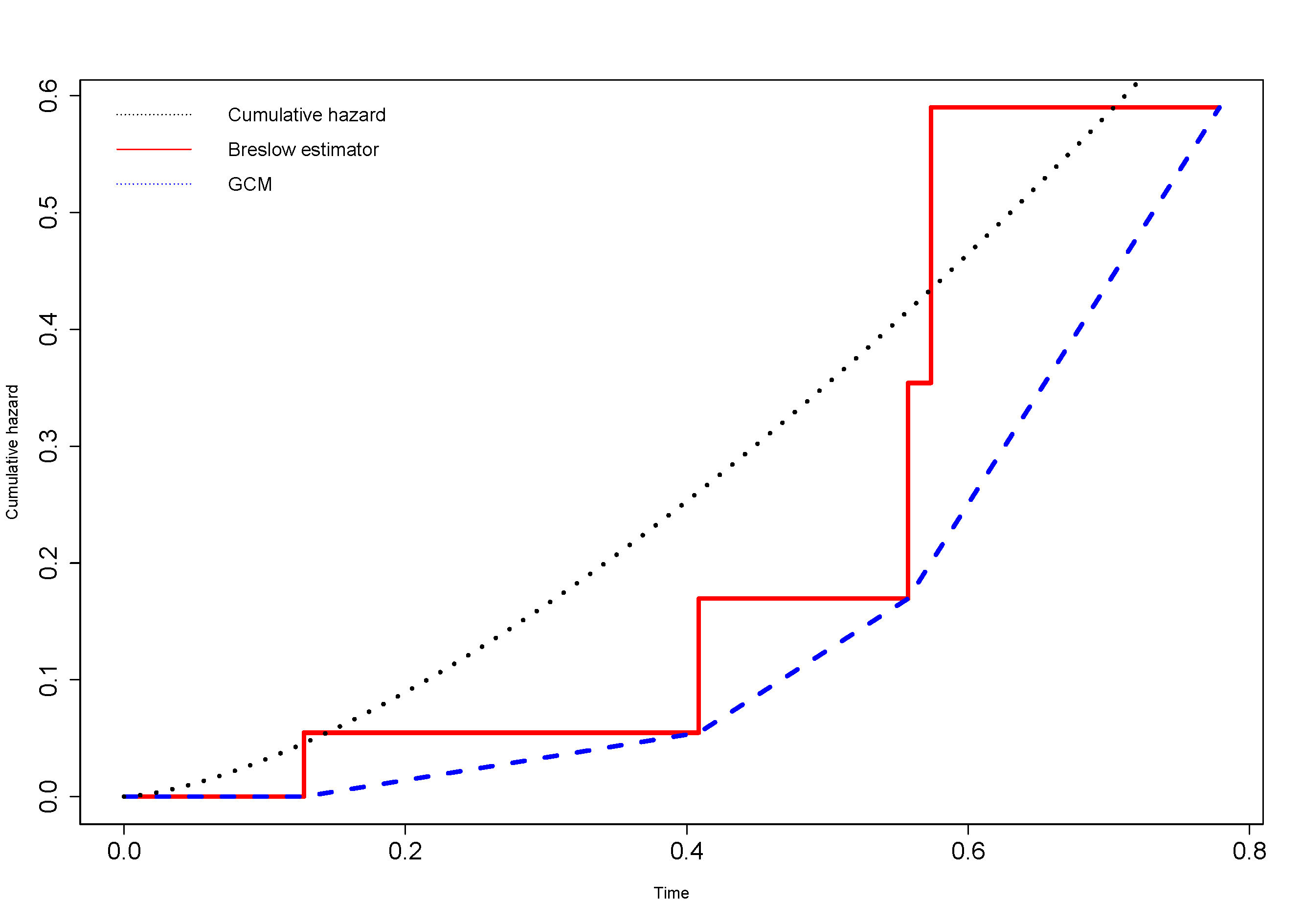
Nonparametric estimation under shape constraints is currently a very active reseach
area in statistics. In particular, in survival analysis, a frequently encountered problem
is the estimation of the hazard rate or of the density function. In this context,
monotonicity constraints arise naturally from the practical expectations. On the other
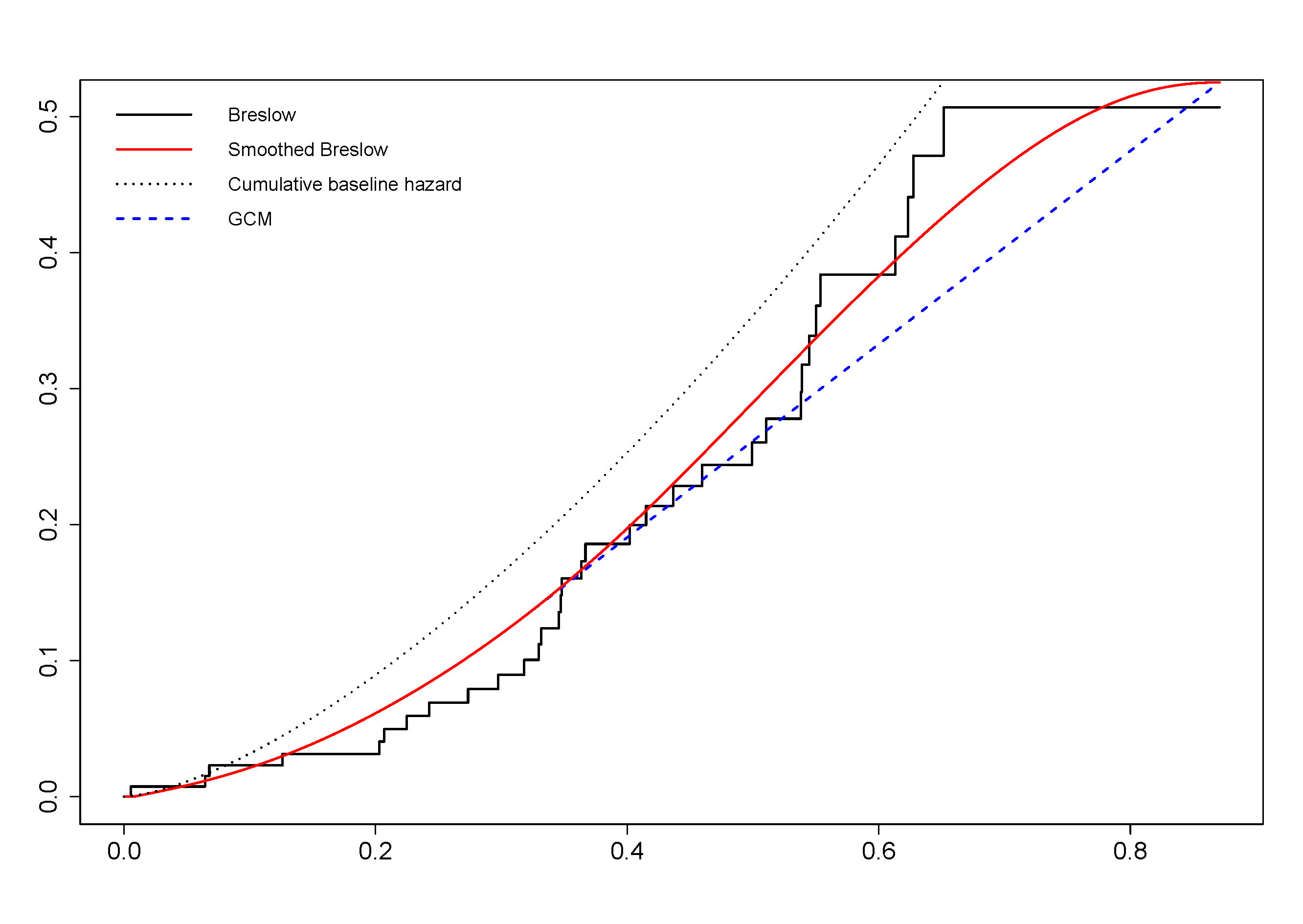
hand, smooth estimators are usually preferred to piecewise constant ones (which result
from traditional methods) because they can be used to achieve a faster rate of convergence
to a Gaussian distributional law and to estimate derivatives of the function of
interest. Kernel smoothing seems to be a rather simple and broadly used technique.
This project focuses on smooth shape constrained methods, taking into account both
the development of theoretical properties as well as computational aspects.
Eni Musta