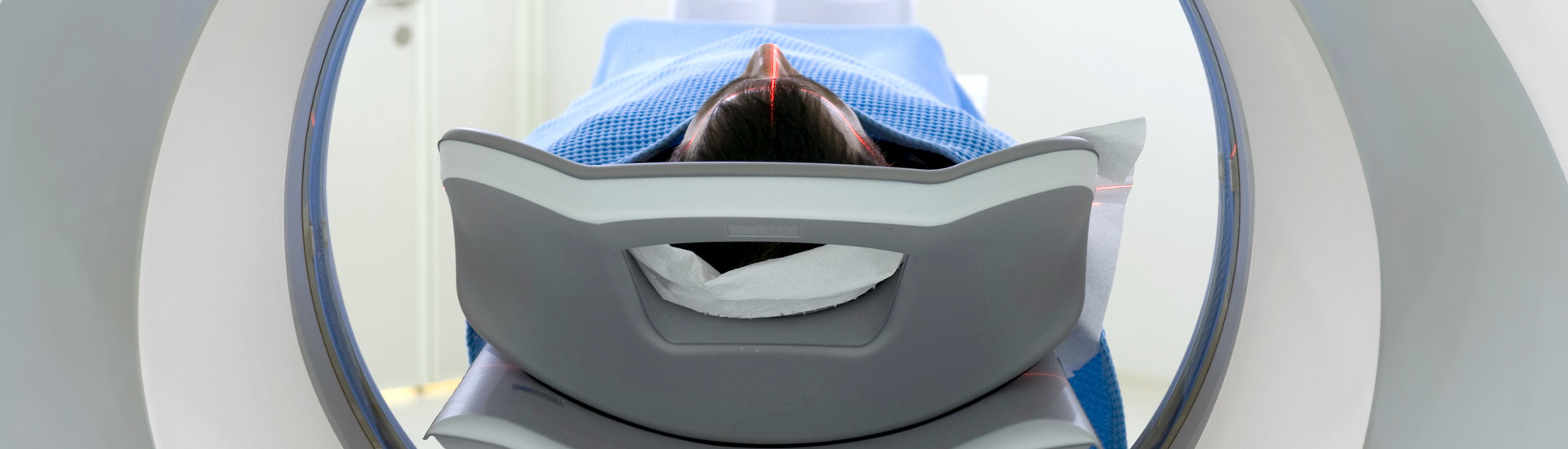
Radiotherapy is often used to treat cancer cells, but all kinds of things can go wrong. An incorrect dosage can damage surrounding tissue, and what do you do if there is an organ in the way? Mathematical models have an important role to play in ensuring that radiotherapy can be conducted with a high level of precision. Marleen Keijzer (lecturer at the Delft Institute of Applied Mathematics) and her former EEMCS student Sebastiaan Breedveld (assistant professor at Erasmus MC) discuss the role of mathematics in an ever-changing field: radiotherapy.
Marleen, what first sparked your interest in mathematics within radiotherapy?
In the mid-1980s, I attended a conference in America on how laser light is used for medical applications. For example, in the case of atherosclerosis, how do you deal with a constricted blood vessel? And how could lasers be used to treat a particular type of cancer? At the time, this was all relatively uncharted research territory. Soon after, I moved from Delft to the United States in order to apply a Monte Carlo method – in other words mathematics – to simulate light scattering. I wrote articles and worked with various hospitals, but decided to return in 1989. Back in the Netherlands, I completed my PhD thesis on calculating light propagation in tissue. If you put a flashlight against your cheek, most of your face will turn red. That is scattered light. But how does the light actually get there? After my PhD, I worked on several more research projects, but soon realised that I much preferred teaching and supervising students with their graduation research. For the latter, the focus was actually always on the useful application of mathematics, for example within radiotherapy.
Final-year students and radiotherapy. What challenges lay ahead of them?
In the field of radiotherapy, it was still possible to make major strides. Graduating students were given all the space needed to design and program their own optimisation methods. An optimised plan of this kind gives you the maximum opportunity to control the tumour and minimise the risk of damage to healthy tissue. So you search for the desired dose distribution and use optimisation to determine how the beams should relate to each other. What happens if you administer one beam here? And what consequences will that have for the dose applied there? Not so long ago, this still had to be done manually: a laboratory technician set the beams, an advanced computer program calculated the dose distribution and the laboratory technician then adjusted the beams to achieve the optimum dose distribution. The problem with radiotherapy is that it doesn’t just involve one single criterion, but numerous conflicting criteria. Optimising a radiotherapy plan could therefore easily take up a whole day.
Sebastiaan Breedveld was one of your graduating students. What exactly did he do?
I supervised Sebastiaan for a while, but he eventually did his PhD research at Erasmus MC – Daniel den Hoed. He was awarded his PhD cum laude on the subject of optimisation. Because laboratory technicians were having to devote a whole day to a radiotherapy plan, Sebastiaan developed a method in which optimisation was fully managed by a computer. An important component of this is the so-called wish list. For some organs, it’s perfectly clear how high the radiation dose can still be. You’re dealing with strict limits. It’s important to take account of these limits, because if the radiation dose is too high, for example in the case of spinal treatment, it may leave the patient paralysed. But the reverse is also true: if you radiate a tumour using less than the minimum dose, it may start to grow back. As well as adhering to strict limits, you need to keep the dose administered to each organ as low as possible. The wish list allows you to do this in a prioritised way (one by one). In order to guarantee quality of life, one organ is sometimes more important than the other. This is something you will also take account of when developing a treatment plan.
So this radiation issue is really about optimisation…
Yes, that’s actually what it comes down to. After all, numerous optimisation methods are being used in radiotherapy. Nowadays, the maths are done by computers. But it still takes time. The graduation students I am now supervising are working to make this process faster and more practical while also tailoring it more effectively to the individual patient. Ideally, you want to fine-tune the plan when the patient is actually lying inside the radiotherapy device. Real time. The human body is always moving, while a radiotherapy plan is made weeks before the start of the first treatment. If the bladder is slightly fuller, it may have pushed an organ or tumour into a slightly different position, for example. With that issue in mind, we had another doctoral candidate develop a statistical model of the movements of the prostate. He analysed numerous CT scans from different patients, identified the most important movements from these and summarised it all in a model. This is a very useful application for mathematics, because as soon as you realise where the uncertainties are, you can start taking them into account. It is a very practical EEMCS issue.
What challenges are there for the future?
Radiotherapy techniques could be customised more. In the 1960s, they would put a piece of lead on a patient, with an opening cut out for the radiation beam at the level of the tumour. This meant that the radiation beam was limited to the tumour alone. Today, everything is done using three-dimensional CT scans, fast computer calculations and highly targeted radiation beams. There has been significant progress, but treatment could still be tailored more effectively to the individual patient. Also, planning methods are still not anything but standard. It would be great if planning methods were generally accepted and made easily accessible, so their use would not be limited to the university hospitals of wealthy countries.
Marleen Keijzer is a lecturer at the Delft Institute of Applied Mathematics, also known as DIAM, at TU Delft. As part of her job, Keijzer is responsible for the first-year course in Mathematical Modelling, and teaching and coaching students is what she enjoys most. In the last decades, Marleen has supervised numerous students during their graduation projects or PhD programmes. Most of her projects were based at the Daniel den Hoed Clinic – now Erasmus MC – and concerned radiotherapy treatment planning. Together with her colleague Theresia van Essen, Marleen is currently setting up an online course In Hands-on Optimisation. Keijzer also recently became vice-chair of the TU Delft Works Council.
Sebastiaan, what first sparked your interest in mathematics within radiotherapy?
I was always eager to do something in the world of medicine. Eventually I opted for a study in Applied Mathematics at TU Delft. But I kept being attracted by the medical field. With that attraction in mind, I decided to do my graduation research on a mathematical issue with a medical application. Because Marleen lectures on the subject, I thought: ‘I would like her to supervise my graduation research!’ Via Marleen, I ended up at Erasmus MC – Daniel den Hoed in Rotterdam.
How did you manage to combine mathematics and radiotherapy there?
Maybe I should tell you something about radiotherapy first. Radiotherapy is used in approximately half of all diagnosed cases of cancer. Radiotherapy is all about irradiating tumours – you’re actually destroying cells. To do that effectively, you need a radiotherapy plan. This plan actually describes the settings for the radiotherapy device that will result in the desired dose distribution. What makes it problematic is that you’re dealing with ionising beams that go straight through a patient. Such a beam actually destroys everything in its path. On the one hand, you of course want to apply enough radiation to be able to eliminate the tumour. But then again, you don’t want to do this at the expense of the surrounding organs: your aim is to minimise the risk of complications as much as possible. Take a tumour in the head and neck area. If you expose the small salivary glands to an incorrect dose during irradiation, this may result in permanent damage. It may lead to a situation where the patient has to drink a little water every 30 minutes, even at night. What dose do you opt for? And how do you then distribute that dose? These are important questions that involve mathematical calculations.
How did you include these questions in your own research?
It’s worth knowing that my research involved two stages. The first stage was to investigate how the available equipment could be used as effectively as possible. In the Netherlands, we've seen a rapid development of most equipment, while the range of possible applications has lagged behind. Smart use of mathematical models enabled us to catch up and put the available equipment to maximum use. The second step was to answer the question: how do you distribute the dose? In order to find out, I asked a number of colleagues: what is it you would like to see in a therapy plan? Based on that input, I compiled a wish list: a list that I could use to guide the optimisation. Running through this wish list, you can work towards a radiation dose that is highly precise based on sophisticated calculations. At that time, the process was relatively new.
For some organs, it’s perfectly clear how high the radiation dose can still be. You’re dealing with strict limits.
How did you apply the wish list in practice?
This wish list ultimately generated automated working methods. Now, there were two plans: one plan that had been developed clinically and one plan generated automatically. In order to find out which method worked best, both a clinical and an automatically generated plan were developed for 50 patients. By doing this, we hoped to achieve some kind of statistical relevance. Both variants were submitted to a doctor who was then asked: which plan would you use to treat this patient? The doctor had not been told which variant had been calculated manually or automatically. After repeating this 33 times, we ended the experiment. We found that in 32 out of 33 cases, the preference was for – what turned out to be – the automatically generated plan. The difference in quality was so convincing that from an ethical perspective we felt compelled to make an effort to treat all patients within this group in the new way. In other words, the wish list worked.
The problem with radiotherapy is that it doesn’t just involve one single criterion, but numerous conflicting criteria.
In the years ahead, what will be the greatest challenge in the field of radiotherapy?
The HollandPTC outpatient centre – based on the TU Delft campus – recently started treating patients using proton therapy. This form of radiotherapy for cancer is new to the Netherlands. Protons are small, positively charged atomic particles that enable high-precision irradiation. This means that less radiation reaches healthy tissues, with a smaller risk of side-effects. TU Delft is working on the technical side of this study. Rotterdam and Leiden manage the medical side. But there’s another question: how can you make a radiotherapy plan even faster and more effective? Imagine you need to make last-minute changes to a plan. How then do you ensure you can go through all those gigabytes of active data as quickly as possible?
Would you ever change the world of radiotherapy for another one?
When I started here, I thought: when I’ve done my bit, I’ll slip away and move into hydraulic engineering. I’ve now passed that point. What makes radiotherapy interesting is that new techniques are continually emerging. For example, proton therapy has been around for a decade, but at Holland PTC, the very first patient was only treated last December. Radiotherapy doesn't essentially solve any problems, it simply creates new opportunities.
Sebastiaan Breedveld studied Applied Mathematics at TU Delft. Both his Master's and PhD research focused on the automation of treatment plans within radiotherapy. Breedveld is now an associate professor at Erasmus MC, where he is continuing his research aimed at improving radiotherapy treatment methods.
Radiation therapy is one of the most important treatments against cancer. One of the ways to do this is through external beam radiotherapy (EBRT). A Linac (a linear particle accelerator) is often used for this treatment. The position of the angles is one of the problems you have to deal with during the preparation of the treatment. In other words: from which directions the patient is going to be irradiated. As you can see in the video, there are different degrees of freedom that can be used and combined. The device in the video is used in the majority of the hospitals. For both traditional and more contemporary treatments, think of proton therapy.