Research
Our goal is to enhance and utilize Quantum Machine Learning in order to develop solutions to real-world problems and to support the development of quantum devices.
Introduction
With the arrival of NISQ (noisy intermediate-scale quantum) technology, four fundamental actors come into play. While physicists and engineers take care of the actual development of qubits and the construction of corresponding hardware, mathematicians, computer scientists and theorists in general are busy pushing the limits of quantum information and quantum algorithms. Domain experts with complex problems and use cases investigate possibilities for the utilization of quantum technologies and vendors create a rich market for software development frameworks, programming languages and libraries.
Immense research activity can be seen in this mixture, many questions are answered in a groundbreaking way and just as many new questions arise. Each of the research domains listed above has got questions for itself, but there are always those that connect to other domains. And it is precisely in this construct that our group finds itself and researches quantum machine learning paired with a strong background in (theoretical) physics.
Fundamental research questions pursued by the group are:
- How can the error model of a quantum device be learning (> hardware)?
- How can quantum error correction be made adaptable (> information and algorithms)?
- How can a hybrid calculation be implemented (> development environment) in order to solve problems that are as realistic as possible (> use cases)?
The successfully completed and also currently ongoing efforts of the Quantum Machine Learning group can be further broken into the research fields of Quantum Computer Architecture, Quantum Gate Set Tomography and Quantum Error Correction. In addition to this rather theoretical research, which is oriented towards the quantum device itself, we also target the practical application, namely Quantum Software Engineering, Problem Transformation and (Meta-)Heuristic Optimization. Areas of application are in particular financial optimization, graph-theoretical problems, time series analysis and game theory.
Full-Stack Quantum Computing
We don’t see quantum computing as a black box, but as a realization of a special computer architecture including several layers. At the lowest level, n-qubit registers are developed (> integration technology). Those are driven by means of analog control and read-out electronics (> electronics). Based on these hardware layers, several software layers follow. With strong reference to the quantum technology incorporated, quantum execution and error correction are carried out, followed by a generalization using quantum instruction set architecture. The compiler and runtime layer pursue multiple tasks such as decomposing, optimizing, mapping and scheduling given circuits. Finally, there is the top layer of quantum algorithms, in which relevant applications for solving real-world problems are addressed.
To conclude: On the one hand, our group utilizes machine learning techniques to support the development of the layers mentioned (i.e., machine learning for quantum). On the other hand, the group uses the results and benefits of all layers to provide solutions to domain experts (i.e., quantum machine learning).
Current Activities
Characterization and Simulation of Noisy Quantum Computation (PhD thesis, Abid Moueddene)
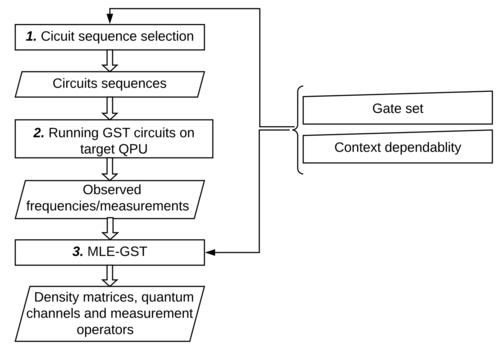
The aim of this project is the implementation and evaluation of quantum algorithms under the influence of noise and Quantum Error Correction Codes (QECC). For this purpose, quantum chips are characterized using Gate Set Tomography (GST). These GST-based error models, including leakage errors and non-Markovian behavior, are integrated into a quantum simulator. Future work includes the analysis of spatial-temporal effects using unsupervised learning techniques that are capable of handling incomplete, partially observable, dynamic, continuous and stochastic environments.
Design Space Exploration Methodologies for Efficient Mapping of Quantum Circuits (PhD thesis, Medina Bandic)
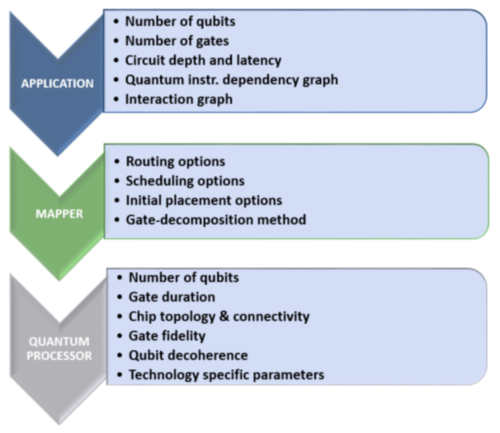
The overall goal is to create an efficient, AI-based quantum computing architecture that incorporates neutral qubit routing as well as scalability with respect to multi-core quantum architectures. For this purpose, a gap analysis using structured Design Space Exploration (DSE) is carried out in order to obtain requirements and challenges of current mapping techniques in particular with reference to multi-core-scaling and communication awareness. The structural comparison of existing mapping solutions including different quantum technologies sheds light into the relationship between algorithm groups and device properties. Based on this, mapper optimizations are proposed. Since generalization and scalability is always considered, these finding are suitable to foster chip design based on mapper algorithms and their properties. Future work includes investigating techniques from the domains of multi-agent and distributed systems, graph-theoretical and clustering algorithms as well as reinforcement learning.
Automation Perspectives on QEC in the NISQ-Era (PhD thesis, Matthew Steinberg)
The main goal of this project is to investigate high-level automation techniques for the control and regulation of the entire Fault-Tolerant Quantum Error Correction (FT-QEC) process. To address automation first, quantum algorithms are characterized in the context of qubit mapping in order to understand the mutual dependence of mapping solutions and the type of quantum algorithm. This is used to develop a taxonomy for the characterization and classification of quantum algorithms. In the next step, we investigate QEC in the Flag-FT regime and in particular the potential of optimality for NISQ-era devices. The motivation behind is the desire for designing quantum architectures that are optimal for the FT-QEC process. Based on these findings, attempts are being made to develop qubit mapping algorithms especially for small QEC codes (QECCs). To do this, we carry out profile and control QPU noise channels before we map those small QECCs. Additionally, we examine whether a generalization of qubit mapping is possible for different QEECs. Ultimately, the endeavors lead to the development of automation techniques for independent and adaptive FT-QEC processes. Future work include the use of (meta-)heuristics for spatial-temporal optimization and the use of adaptive algorithms in uncertain environments.

