Excavation of Hard Deposits and Rocks (EXHADERO)
Rudy Helmons
Introduction
A variety of rock cutting technologies is used in marine environments, e.g. dredging, deep sea mining and oil/gas drilling. Rock cutting is the fracturing and disintegration of a rock under mechanical action of a cutting tool. When rock is cut at large water depths, the high hydrostatic pressure complicates the cutting process. Rock that behaves brittle under atmospheric conditions will behave in a more ductile fashion. Therefore, the influence of pore and hydrostatic pressure needs to be considered in the analysis of the rock cutting process.
Cutting Process
A cut starts with an indention of the tool. Because of the strength of the overburden, the indention is contained and the zone near the indention fails cataclastically, creating a crushed zone. With further indention, the size of the crushed zone increases until a shear crack occurs at the boundary of the crushed zone. This shear failure will then bifurcate into a tensile crack, which results in chip formation, see figure above. Due to the high deformation rates that can be applied in the rock cutting process, the effective stress will change locally in case of (partially) undrained behavior. As a result the bulk properties of the rock are rate and pressure dependent and the cutting process will become more ductile.
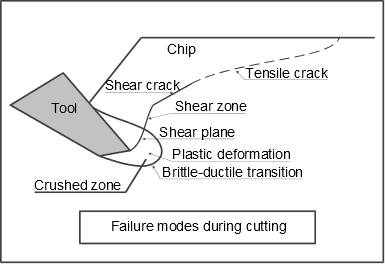
Phenomenological cutting model, based on Van Kesteren [1]
Modelling Approach
The numerical model of the cutting process has been developed within the framework of the Discrete Element Method (DEM). In DEM, the solid material is represented as a collection of particles that have mutual interactions in normal and tangential directions. Rock is modelled using the elastic perfectly brittle model of contact interaction, in which initial bonding between neighboring particles is assumed. The bonds can be broken under excessive load, which allows to simulate initiation and propagation of material fracture (both tensile and shear). When a bond is broken, contacts are treated assuming a standard contact model with Coulomb friction.

Left: bond in normal direction, middle: bond in tangential direction (contact after failure), right: bond in tangential direction (no contact after failure)
Due to the high deformation rate and the low permeability of the rock, it is assumed that the relative fluid velocity is negligible and as a result, the fluid pressure is modeled with the pressure diffusion equation:
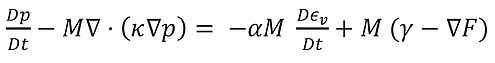
With pressure p, time t, Biot modulus M, permeability κ, effective stress coefficient α, volumetric strain εv, fluid source γ and force F.
In order to convert the discontinuous properties of the particles in DEM to a continuum field, the Smoothed Particle (SP) approach is used. Coupling between the methods is applied every time step by calculating the volumetric strain rate (DEM) and the pressure gradient force (SP).
Preliminary Results
The combined DEM-SP approach is used to do various tri-axial compression tests with initial equilibrium. All experiments were done on the same type of rock, only the presence of a pore fluid and the hydrostatic pressure are varied.

Simulation drainage related phenomena in compression tests
Qualitative results show various effects (see figure above):
- Stiffening: the rock skeleton stiffens due to the presence of the pore fluid.
- Compaction weakening: due to the compaction of the rock, the pore pressure inside the rock becomes higher than the confining pressure. As a result the apparent strength of the rock reduces.
- Dilatancy hardening: fluid needs to flow into the opening macroscopic cracks. This results in a pressure gradient that counteracts the opening of the cracks. However, the pressure in the cracks has a lower limit, that is when the fluid pressure drops to the vapor pressure of the fluid, i.e. cavitation occurs.
The stiffening of the saturated rock in the undrained regime (κ=0) corresponds well with the Biot-Gasmann theory for the relation between the drained and undrained bulk modulus of the saturated rock (see figure below).
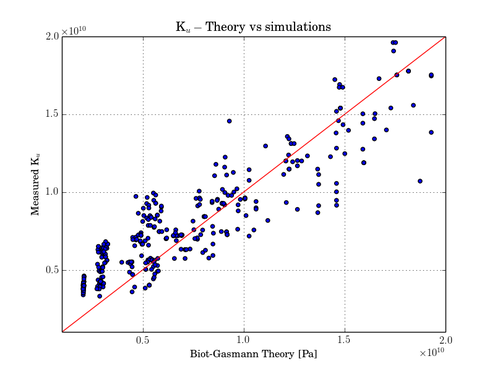
Undrained stiffness simulations vs. Biot-Gasmann theory
Simulations of the dry (drained) and hyperbaric (undrained, ph >> UCSrock) rock cutting processes correspond qualitatively with the theory. These simulations clearly show the distinction between brittle and ductile cutting, see figure below.

Colors depict the amount of damage done to each particle, red means no damage at all, blue means that all bonds with neighboring particles have been broken.
Conclusions
The newly developed method is able to model:
- Mechanics of saturated rock; phenomena like dilatancy hardening, compaction weakening and undrained behavior are clearly observed.
- Rock cutting process; qualitatively the brittle-ductile transition is noted (atmospheric vs. hyperbaric). The model agrees well with literature.
Future Research
The model will be further improved to enable the model to more accurate predictions. Extension to 3D simulations might be necessary to do this.
Acknowledgements
This research is part of a collaboration between Delft University of Technology, Agentschap NL, Royal Dutch Shell, Royal Boskalis Westminster NV, Van Oord Dredging and Marine Contractors BV and Royal IHC Merwede.