One-class Classification
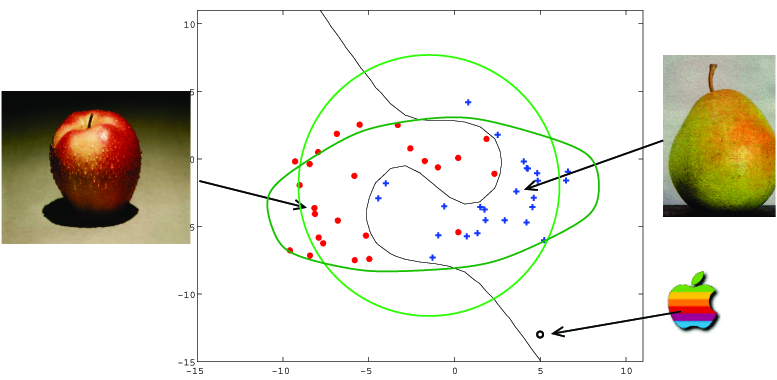
In contrast with normal classification problems where one tries to distinguish between two (or more) classes of objects, one-class classification tries to describe one class of objects, and distinguish it from all other possible objects. In the figure below an example data set is shown, representing a set of apples and pears. The objects can be classified well by the classifier, but the outlier in the lower right corner will be classified as a pear. A one-class classifier should then be trained to reject this object and to label it as an outlier.
This one-class classification can be applied in different problems. It can be used for:
1. Novelty detection (for machine condition monitoring where faults should be detected),
2. Outlier detection (for more confident classification as in the example above),
3. Badly balanced data (classification in medical data with poorly sampled classes),
4. Data set comparison (to avoid the training classifiers again for comparable data).
Often just the probability density of the training set is estimated. When new objects fall under some density threshold, this new object is considered outlier and is rejected. We propose a method which does not rely on density estimation. The method is inspired on the Support Vector Machine by V.Vapnik. It computes a spherically shaped decision boundary with minimal volume around a training set of objects. This requirement (and the constraint that all objects are within the sphere) results in a description in which the sphere is described by just a few objects from the training set, called Support Objects. Instead of storing the complete training set, just this much smaller set of support objects has to be stored. The spherical description can be made more flexible by introducing kernel functions, analogous to the Support Vector Machines. When a Gaussian kernel is used (with an extra free parameter s) solutions ranging from a Parzen density estimation to the original spherical description are obtained. Also a procedure for choosing the appropriate value for s is given such that for all types of data a tight description can be obtained.
These tools can now answer other questions. It can solve the classification problems in which the different classes are very poorly balanced (or in which one of the classes is completely absent). This happens in medical applications where the population of normal, healthy people is far bigger than the abnormal population. It also opens the possibility to give an indication that a test set is sufficiently similar to the training set.