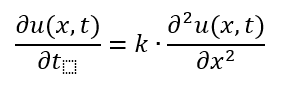Ruis voegt willekeurige verstoringen toe aan allerlei processen, zowel fysisch als economisch. Signalen en (meet)waarden die eigenlijk constant zouden moeten zijn, of relatief traag variëren, krijgen hierdoor een zeer grillig verloop. Onvoorspelbaar als ruis is, de invloed ervan kan wel degelijk gemodelleerd worden. En met het juiste wiskundige inzicht is zo’n model dan nog oplosbaar ook.
Ruis op elke schaal
Mark Veraar, professor in de Analysis groep van het Delft Institute for Applied Mathematics (DIAM), heeft een brede wiskundige interesse en werkt graag op meerdere deelgebieden tegelijk. Al sinds zijn promotie is ook ruis een belangrijk deel van zijn onderzoek. ‘Ruis zien we overal om ons heen, op elke schaal,’ zegt hij. ‘Van kwantumfluctuaties op het niveau van elementaire deeltjes, via de willekeurige beweging van stofdeeltjes in een gas of vloeistof, tot aan turbulentie in de atmosfeer en in klimaatmodellen. Maar bijvoorbeeld ook in de economie, zoals een plotselinge uitschieter op de financiële markten of de schommelingen in de koers van een aandeel. Zelfs afrondfouten in een computer zijn een vorm van ruis.’ Niet alleen is de wereld om ons heen ervan doordrongen, ruis kan zelfs een doorslaggevende invloed hebben in en op de modellen die ingenieurs en andere wetenschappers maar al te graag gebruiken om voorspellingen te doen over deze wereld. De door een klimaatmodel voorspelde zeespiegelstijging van een paar meter komt waarschijnlijk door (gemodelleerd) menselijk handelen. Het kan echter, bij wijze van spreken, ook het gevolg zijn van een ogenschijnlijk onschuldige afrondfout die uit de hand loopt. ‘Door ruis er specifiek in mee te nemen, sluit zo’n model beter bij de praktijk aan en kan je bovendien iets zeggen over de kans op dat onbedoelde gedrag,’ legt Veraar uit. ‘Om diezelfde reden onderzoek ik ook vaak het lange termijngedrag van de oplossingen. Ontstaat er een evenwicht, en hoe snel gebeurt dat?’
Stuiterend stuifmeel
‘Voor het modelleren van ruis in problemen die in de natuurwetenschap en in de economie voorkomen, gebruik ik de wiskunde van de Brownse beweging,’ zegt Veraar. De Brownse beweging is het fenomeen dat kleine deeltjes, zoals stuifmeel, in water een ogenschijnlijk willekeurig pad afleggen als gevolg van vele random botsingen met de nog veel kleinere watermoleculen. De wiskundige beschrijving hiervan is al meer dan honderd jaar oud, en nog steeds worden nieuwe eigenschappen ontdekt. ‘Op deze manier gemodelleerd is de ruis onvoorspelbaar en heeft het overal een gelijke intensiteit,’ aldus Veraar. Bij een klimaatmodel betekent dit bijvoorbeeld dat de invloed van ruis niet afhangt van de locatie op aarde waar je kijkt, en ook niet van wanneer je daar kijkt.
Zachte en harde technieken
Wiskundigen blijven met een model het liefst zo dicht mogelijk bij de werkelijkheid, en ruis is dan een belangrijke toevoeging. Dikwijls vormen zogenoemde partiële differentiaalvergelijkingen de basis zo’n model (zie kader). Pittige kost, maar als voormalig beste docent van de EWI faculteit# weet hij geduldig en duidelijk uit te leggen. ‘Een model is nog geen oplossing,’ zegt hij. ‘Waar het bijvoorbeeld voor een vliegtuigbouwer overduidelijk is dat er in de windtunnel een bepaalde luchtstroming om zijn experimentele vleugelontwerp loopt, is het lang niet altijd mogelijk daar op basis van het wiskundig model veel over te zeggen.’ Het gaat hem bij zijn onderzoek om fundamenteel begrip van de vergelijkingen, inclusief ruis. Hierbij past hij zowel zachte als harde wiskundige methoden toe. ‘Dat heeft niks met makkelijk en moeilijk te maken, maar meer met hoe efficiënt je iets over situaties kan zeggen,’ legt hij uit (zie kader). ‘Het bestaan van een optimum – een best mogelijke uitkomst – is vaak heel makkelijk zacht te bewijzen, met een paar formules bijvoorbeeld. Het vinden van dat optimum met een efficiënt algoritme is soms juist heel moeilijk. Maar soms is zachte wiskunde juist veel moeilijker. In mijn onderzoek probeer ik zo lang mogelijk gebruik te maken van zachte technieken, totdat het echt niet meer kan.’ Dan biedt een technische afschatting of numerieke benadering op de computer mogelijk uitkomst.
Partiële differentiaalvergelijking (PDV)
Een relatief eenvoudig voorbeeld van een PDV is de warmtevergelijking waarmee de temperatuurverdeling in een één-dimensionale staaf wordt beschreven, en hoe deze over tijd verandert.
De functie u(x,t) geeft de temperatuur in in alle punten x op tijdstip t. Links van het gelijkteken staat de afgeleide van u(x,t) naar de tijd – hoe snel verandert de temperatuur op punt x, in graden per seconde. Rechts staat de tweede afgeleide naar de plaats – als ik in de buurt van punt x kijk, neemt de snelheid waarmee de temperatuur verandert dan juist af of toe. De warmtevergelijking is een exacte beschrijving van de oplossing, zonder dat het de functie u(x,t) geeft, en dus de oplossing zelf.
Harde en zachte wiskunde
Voor het optellen van de getallen 1 tot en met 100 is een zachte wiskundige aanpak veel efficiënter.
Hoe meer we weten over de gladheid van een functie, hoe efficiënter we deze numeriek kunnen benaderen.
Met gladheid op weg naar de oplossing
Dankzij de sterk toegenomen rekenkracht van computers kunnen ingenieurs en andere wetenschappers al gebruik maken van steeds realistischer wiskundige modellen van processen. ‘Het benodigde rekenwerk voor een numerieke benadering kan echter nog steeds buitensporig hoog zijn,’ zegt Veraar. ‘Maar hoe meer inzicht we hebben in de eigenschappen van de oplossing, hoe slimmer we de computer aan het werk kunnen zetten, zodat het rekenwerk niet uit de hand loopt.’ Hij duikt hiervoor graag de wiskundige diepten in. Zo houdt hij zich onder andere bezig met het beschrijven van de “gladheid” van een oplossing. De wiskundige term daarvoor is regulariteit en het geeft aan hoe vaak je van een functie de afgeleide kan bepalen (een maat voor hoe snel een functiewaarde varieert - zie kader), en of deze afgeleide functies zich ook weer netjes gedragen. ‘Juist deze gladheid kan je gebruiken bij het implementeren van efficiënte numerieke benaderingen,’ zegt Veraar.
Door ruis specifiek mee te nemen, sluit een model beter bij de praktijk aan.
Diepe connecties
Zijn huidige onderzoek ligt op het snijpunt van drie wiskundige deelgebieden (functionaalanalyse, harmonische analyse en de kansrekening) en heeft Veraar veel gebracht. ‘Heel diep in de theorie vind ik connecties tussen deze deelgebieden die ik niet zomaar had verwacht.’ Voor een wiskundige zijn dat fijne eureka-momenten. Voor een vliegtuigbouwer betekent het dat hij een volgende keer misschien geen schaalmodel hoeft te bouwen om in een windtunnel door te meten. Toch overweegt Veraar ondertussen alweer een verdere verbreding van zijn kennis. Natuurlijk zorgt zijn dochter van anderhalf jaar voor enige ruis op de lijn, maar begin volgend collegejaar wil hij tijdens een internationale onderzoeks-sabbatical nieuwe ideeën opdoen. ‘Ik weet nog niet precies waar ik dat eerste semester zal doorbrengen. In ieder geval zoek ik een plek waar het onderzoek voldoende met dat van mij overlapt, zodat we elkaar begrijpen. Maar waar het ook genoeg afwijkend is zodat ik een interessant vervolg kan schrijven op mijn huidige VIDI-onderzoek.’ Veraar is nog niet klaar met ruis.
# Mark Veraar is in 2017 verkozen tot beste docent van zowel de opleiding Wiskunde als van de gehele EWI faculteit. Daarnaast is hij driemaal als tweede geëindigd.
Tekst: Merel Engelsman | Portretfoto: Mark Prins