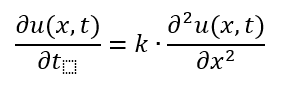Noise adds arbitrary fluctuations to both physical and economical processes. As a consequence, there are many abrupt variations in signals and measured values that should be either constant or varying only relatively slowly. Although noise itself is unpredictable, its influence can certainly be modelled. Using the correct mathematical insights, these models can then be solved.
Noise at any scale
As professor in the Analysis group at the Delft Institute for Applied Mathematics (DIAM), Mark Veraar has a wide range of mathematical interests. Noise has been one of these interests ever since he was a PhD student. ‘Noise is everywhere, at every scale of observation,’ he says. ‘From quantum fluctuations at the level of elementary particles, through random motion of dust particles in a gas or a liquid, to turbulence in the atmosphere and in climate models. Noise is not only a physical phenomenon, it is also a characteristic of economic processes such as a sudden rise in the financial markets or the fluctuations in the price of shares. Rounding errors in a computer are yet another kind of noise.’ It is fair to say that our world is a noisy place. More importantly, noise can have a decisive influence within the models that engineers and other scientists use to make predictions about this world. The few meters rise in sea level as predicted by climate models will most likely be the consequence of (modelled) human activity. But it could, in a manner of speaking, also be due to a seemingly harmless rounding error running out of control. ‘By specifically modelling noise, a model may more closely conform to reality. It also allows us to make statements as to the likelihood of such unwanted behaviour,’ Veraar explains. ‘It is for this reason that I also investigate the long-term behaviour of model solutions. Will an equilibrium be reached, and at what timescale?’
Hopping pollen
‘I use the mathematics of the so-called Brownian motion to model noise in problems in the realms of physics and economics,’ Veraar says. The Brownian motion is the phenomenon that small particles, such as pollen, display a seemingly arbitrary pattern of motion when immersed in water. Their erratic bouncing around is a consequence of many random collisions with the even smaller water molecules. The mathematics of the Brownian motion is over a century old, but new features continue to be discovered. ‘When modelled as such, noise is unpredictable and it will have a uniform intensity,’ Veraar says. In a climate model, for example, this means that the impact of noise does not depend on where you look (the location) or when you look (at what modelled time).
Hard and soft techniques
Mathematicians like their models to be as close to reality as possible, making noise an important ingredient. Such models are often based on so-called differential equations (see frame). Not the easiest subject matter to wrap your head around, but as a former best teacher of the faculty of EEMCS# Veraar knows how to explain patiently and clearly. ‘A model and its solution are two entirely different things,’ he says. ‘It may be clear for an aircraft engineer that, when put in a tunnel, his experimental wing design results in a certain airflow. Using a mathematical model, however, it isn’t always possible to make any statements about that airflow.’ Veraar is interested in a fundamental understanding of the underlying equations, including noise. In his research, he applies both soft and hard mathematics (see frame). ‘Soft and hard has no relationship to the mathematics being simple or difficult,’ he explains. ‘Rather, it is an indication of how efficiently you can make statements about a certain mathematical situation. It is often relatively easy to prove the existence of an optimum – a best possible outcome – using soft mathematics. Defining an efficient algorithm to find that optimal solution can, however, be very difficult. But sometimes it is much more difficult to use soft mathematics. In my research I try to stick with soft techniques, resorting to hard techniques only when absolutely necessary.’ At such a moment, a computer may be required to perform a numerical approximation or a technical estimation.
Partial Differential Equations (PDE)
A relatively simple example of a PDE is the heat equation. It describes the temperature distribution in a one-dimensional rod and how it changes over time.
The function u(x,t) describes the temperature for each coordinate x at time t. On the left of the equal sign you find the time derivative of u(x,t) – how quickly does the temperature at point x vary, in degrees per second. On the right side you find the second derivative to the location – if I look in the neighbourhood of x, do I observe an increase or a decrease in the speed with which the temperature changes. The heat equation is an exact description of the solution. It does, however, not give you the function u(x,t), and thereby the solution.
Hard and soft mathematics
A soft mathematical approach is much more efficient for adding the numbers 1 to 100.
The more we know about the smoothness of a function, the more efficient we can approximate it with numerical methods.
A smooth solution
Thanks to the ever-increasing computational power, the mathematical models used by engineers and other scientists have become more and more realistic. ‘It may, however, still be the case that a prohibitively large number of calculations is required to approximate the solution of a model,’ Veraar says. ‘The better understanding we have of the properties of a solution, the more efficient an algorithm we can implement, thereby staying within computational limits.’ To attain such understanding, Veraar enthusiastically explores the depths of mathematics. One of the aspects he delves into is the so-called “smoothness” of a solution. In mathematical terminology this is called “regularity” and it is an indication for how often one can determine the derivative of a function (a measure for how quickly a function value varies, see frame), and whether or not these derivatives are “well-behaved”. ‘It is especially this smoothness of a solution that allows the implementation of efficient numerical approximations,’ Veraar explains.
By specifically modelling noise, a model may more closely conform to reality.
Deep connections
His current research interests are at the cutting edge of three mathematical research areas (functional analysis, harmonic analysis and probability theory) and have been quite a treasure trove. ‘At a very fundamental level I have found unexpected connections between these research areas,’ he says. For a mathematician these are satisfying eureka-moments while for an aircraft engineer it may mean that, next time, he may not have to build a scale model and put it in a wind tunnel. Nevertheless, Veraar is already considering a further expansion of his knowledge. His one-and-a-half-year-old daughter adds some very positive noise to his plans, but he may use the first semester of the upcoming academic year for an international research sabbatical. ‘I don’t yet know at what university I wish to broaden my perspective. There has to be sufficient overlap between their ongoing research and mine, so that we can understand each other. On the other hand, their interests should also be sufficiently dissimilar to allow me to write an interesting follow-up project proposal to my currently ongoing VIDI-grant.’ Wherever he may end up, noise will still be on his mind.
# In 2017, Mark Veraar was voted best teacher of the department of mathematics as well as of the entire EEMCS faculty. He has been the runner-up three times.
Text: Merel Engelsman | Portrait photo: Mark Prins